Stock Selection Optimization
Pickstock is an optimization model from the financing sector. The goal is to pick a small subset of stocks together with some weights, such that this portfolio has a similar behavior to our overall Dow Jones index.
Data:
Performance (price) data of all 30 shares of the Dow Jones index over a period of 1 year:
| Date | Stock | Price |
|---|---|---|
| 2016-01-04 | AAPL | 105.35 |
| 2016-01-04 | AXP | 67.59 |
| 2016-01-04 | BA | 140.5 |
| 2016-01-04 | CAT | 67.99 |
| 2016-01-04 | CSCO | 26.41 |
| 2016-01-04 | CVX | 88.85 |
| 2016-01-04 | DD | 63.07 |
| 2016-01-04 | DIS | 102.98 |
| 2016-01-04 | GE | 30.71 |
| 2016-01-04 | GS | 177.14 |
| […] | […] | […] |
Goal:
The goal is to find a small selection of stocks that follows the Dow Jones as good as possible. The interesting part is not how good the model performs with the data it knows about but how well it approximates the Dow Jones index in the future. In order to simulate this the stock data is devided into two parts: the training phase and the testing phase. The training phase is be the model input data, i.e. the data the model uses to find an index fund to approximate the Dow Jones index as good as possible. When the model finds a solution, the results can be evaluated in the testing phase.
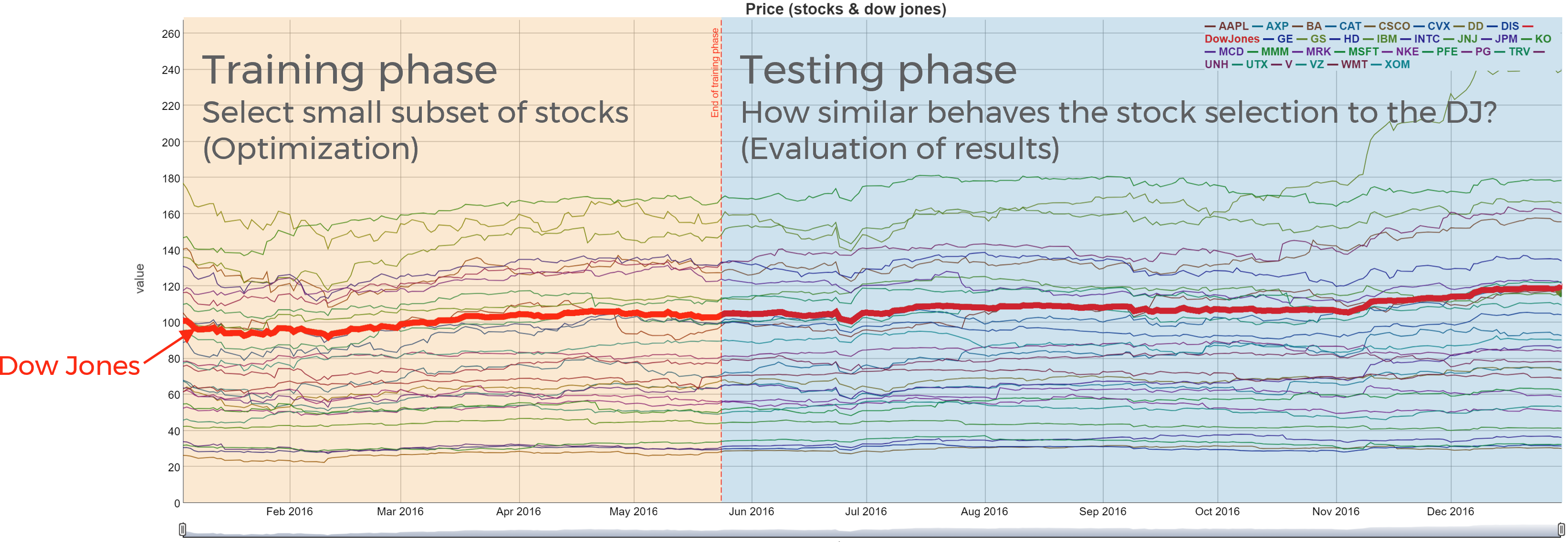
The data of the testing phase is not used for the optimization but only for the evaluation. Since the objective function minimizes the absolute deviation between the DJ index and the selected stocks,the area between the two lines shows how good the solution is.
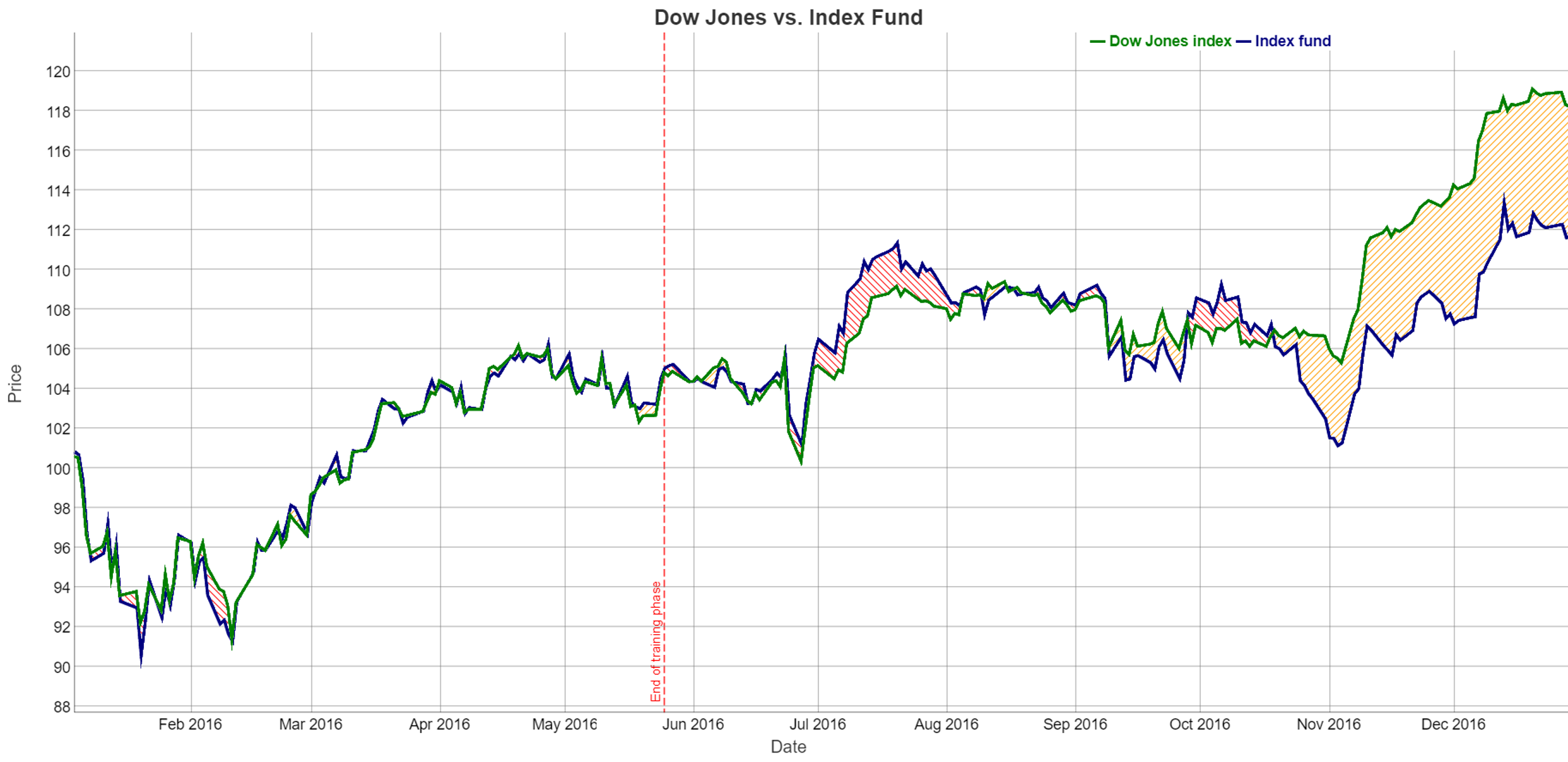
Optimization model:
Select a subset (≤ maxstock) of Dow Jones stocks, along with weights, so that this portfolio behaves similarly to the overall index (in the training phase). The model is based on a linear regression over the time series, but it minimizes the loss using the L1-norm (absolute value), and allows only a fixed number of weights to take nonzero variable.
$$\text{minimize} \qquad \text{obj}:= \sum_{ds} \text{slpos}_{ds} + \text{slneg}_{ds} $$
$$\text{subject to} \qquad \sum_{s} \text{price}_{ds, s} \cdot w_{s} = \text{index}_{ds} + \text{slpos}_{ds} - \text{slneg}_{ds} \quad (\forall{ds})$$
$$w_{s} \leq p_{s} \quad (\forall{s}) $$
$$\sum_{s}{p_{s}} \leq \text{maxstock}$$
$$w_{s}\geq 0, \qquad p_{s}\in \{0,1\} \quad (\forall s)$$
$$\text{slpos}_{d}\geq 0, \qquad \text{slneg}_{d}\geq 0 \quad (\forall d) $$
Important Sets and Parameters:
Set date 'date'
symbol 'stock symbol';
Parameter price(date<,symbol<) 'Price';
Scalar maxstock 'maximum number of stocks to select' / 2 /
trainingdays 'number of days for training' / 99 /;
Alias (d,date), (s,symbol);
The price data is provided by a CSV file:
$setNames "%gams.input%" fp fn fe
$if not set fileName $set fileName %fp%dowjones2016.csv
$call.errorlevel csv2gdx "%fileName%" output=stockdata.gdx ValueDim=0 id=price Index="(1,2)" Value=3 UseHeader=y
$gdxin stockdata
$load price
Definition of the two phases training days and testing (non-training) days:
Set td(date) 'training days'
ntd(date) 'none-training days';
td(d) = ord(d)<=trainingdays;
ntd(d) = not td(d);
The mean price per stock is calculated which can be used in order to calculate weights:
Parameter
avgprice(symbol) 'average price of stock'
weight(symbol) 'weight of stock';
avgprice(s) = sum(d, price(d,s))/card(d);
weight(symbol) = avgprice(symbol)/sum(s, avgprice(s));
Computation of the contributions using weight and price:
Parameter contribution(date,symbol) 'contribution of stock on date';
contribution(d,s) = weight(s)*price(d,s);
Computation of index values:
Parameter index(date) 'Dow Jones index';
index(d) = sum(s, contribution(d,s));
Variables and equations:
Variable
p(symbol) 'is stock included?'
w(symbol) 'what part of the portfolio'
slpos(date) 'positive slack'
slneg(date) 'negative slack'
obj 'objective';
Positive variables w, slpos, slneg;
Binary variable p;
Equation
deffit(date) 'fit to Dow Jones index'
defpick(symbol) 'can only use stock if picked'
defnumstock 'few stocks allowed'
defobj 'absolute violation (L1 norm) from index';
deffit(td) .. sum(s, price(td,s)*w(s)) =e= index(td) + slpos(td) - slneg(td);
defpick(s) .. w(s) =l= p(s);
defnumstock .. sum(s, p(s)) =l= maxstock;
defobj .. obj =e= sum(td, slpos(td) + slneg(td));
Model declaration and solve statement:
Model pickStock /all/;
option optCR=0.01;
solve pickStock min obj using mip;
Reporting parameters:
Parameter
fund(date) 'Index fund report parameter'
error(date) 'Absolute error';
fund(d) = sum(s, price(d, s)*w.l(s));
error(d) = abs(index(d)-fund(d));
Set fHdr 'fund header' / dj 'dow jones','index fund' /
errHdr 'stock symbol header' / 'absolute error train', 'absolute error test' /;
Scalar error_train 'Absolute error in entire training phase'
error_test 'Absolute error in entire testing phase'
error_ratio 'Ratio between error test and error train'
Parameter
stock_weight(symbol) 'weight'
dowVSindex(date,fHdr) 'dow jones vs. index fund'
abserror(date,errHdr) 'absolute error'
priceMerge(date,*) 'Price (stocks & dow jones)';
stock_weight(s) = w.l(s);
dowVSindex(d,'dj') = index(d);
dowVSindex(d,'index fund') = fund(d);
abserror(td, 'absolute error train') = error(td);
abserror(ntd,'absolute error test') = error(ntd);
priceMerge(d,symbol) = price(d,symbol);
priceMerge(d,'DowJones') = index(d);
error_train = obj.l;
error_test = sum(ntd, error(ntd));
if(error_train > 0,
error_ratio = error_test/error_train;
else
error_ratio = inf;);
Hypercube analysis script:
The Hypercube analysis script allows your to analyse a large number of scenarios to answer high-level questions like How many stock should I pick? or How many training days should I choose?.
This analysis script relies on Python to be installed on your machine. In addition, the GAMS Python API is required as well as the following Python packages:
- notebook
- pandas
- matplotlib
The latter can be installed via pip install notebook pandas matplotlib.